教授好像真的是很想教会我们
伯努利分布
伯努利试验是只有两种可能结果的单次随机试验,即对于一个随机变量X而言:
- P[x = 1]=μ
- P[x = 0]=1-μ
伯努利试验都可以表达为“是或否”的问题。例如:
- 抛一次硬币是正面向上吗?
- 今天的实验课老师会点名吗?
- 明天会下雨吗?
If we know µ we can generate output that is similar to what the actual system does, this means we can predict how the system behaves.Now we want to use examples of the systems predictions training data find µ. So far we have onlyset the likelihood for one data-point, what about when we see lots of them? Now we will make our first assumption, we will assume that each output of the system is independent. This means that we can factorise the distribution over several trials in a simple manner
现在不妨假设每次实验都是独立的,当我们进行n次实验时,便可以获得如下的概率分布,称这一串重复的独立试验为n重伯努利试验:
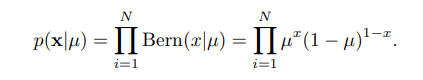
先验概率
In order to say something about the system we need to have a prior belief about what we think the parameter µ is.
为了说明系统,我们需要对我们为系统指定一个先验概率µ。 通俗的讲,先验概率就是事情尚未发生前,我们对该事发生概率的估计。利用过去历史资料计算得到的先验概率,称为客观先验概率; 当历史资料无从取得或资料不完全时,凭人们的主观经验来判断而得到的先验概率,称为主观先验概率。例如我们认为抛一枚硬币头向上的概率为0.5,这就是先验概率。 所谓先验概率,就是我们主观对系统设定的一个先验分布,现在就来说说先验分布。先验分布就是你在取得实验观测值以前对一个参数概率分布的主观判断,不论是否有历史资料支撑,先验分布都需要我们主观进行计算与设定,这也就是为什么贝叶斯统计学一直不被认可的原因,统计学或者数学都是客观的,怎么能加入主观因素呢?但事实证明这样的效果会非常好! 拿掷硬币的例子来看,在扔之前你会有判断正面的概率是50%,这就是所谓的先验概率,但如果是在打赌,为了让自己的描述准确点,我们可能会说正面的概率为0.5的可能性最大,0.45的几率小点,0.4的几率再小点,0.1的几率几乎没有等等,这就形成了一个先验概率分布。
后验概率
后验概率是指通过调查或其它方式获取新的附加信息,利用贝叶斯公式对先验概率进行修正,而后得到的概率。事情发生可能有很多原因,判断事情发生时由哪个原因引起的概率叫后验概率。
比如今天上课你没有去,原因有两个,可能是睡过了,也可能是故意翘课。上课时老师点名发现你没来。(这里是一个结果,就就是你没来学校这件事情已经发生了)老师要计算一下概率,分别是因为生病了没来学校的概率和自行车坏了没来学校的概率。
很显然,后验概率就是在事情发生后判断由哪一个原因引起的概率。这里的事情是你没来上课,原因有睡过了和故意翘课。
而这就是我们通过机器学习想要得到的数值,通过后验概率,我们可以对现实中的一些情况进行预测。
贝叶斯公式
Once we have specified the prior we can just do Bayes’ rule and get the posterior.
要通过先验概率求得后验概率,必须要借助贝叶斯公式。
这一部分是简单的概率论知识的运用,举一个最典型的例子,也是课上的例题,就是已知检出阳性,在各种条件概率的前提下,求出人确实患病的概率:



可见,贝叶斯方程对于解决这类问题十分实用且快捷:
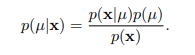
Beta分布
The second thing we will think of is that it does make sense that if I have a prior of a specific form (say a Gaussian) then I would like the posterior to be of the same form (i.e. Gaussian). So this means that we should choose a prior such that when multiplied with the likelihood it leads to a distribution that is of the same form of the prior. So why is this useful? This is very useful because it means we do not have to compute the denominator in Baye’s rule, the only thing we need to do is to multiply the prior with the likelihood and then identify the parameters that of the distribution, we can do this as we know its form.
但是我们无法确认我们的先验概率是完全准确的,如果可以确认,那么就没有机器学习的必要了,所以,我们要不断对我们的模型,根据数据进行更新和维护,但这个更新和维护的计算是十分复杂的,这时,我们就要将目光转到共轭分布,因为在共轭分布中,后验概率分布函数与先验概率分布函数具有相同形式,这时我们仅需进行先验概率与似然性的矩阵乘法,便能得到一个相同形式的后验概率,这就是下一次进行运算的先验概率,以此类推,不断向模型中更新数据,我们便可以获得一个愈加准确的模型。
至于什么分布是共轭分布,留给数学家吧,我不会算。
而这一部分提到的Beta分布就是一个很典型的共轭分布,我们选择了贝塔分布作为先验概率,其概率分布函数为:
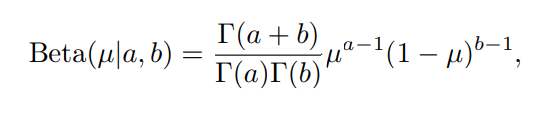
通过一些我非常不擅长的计算,我们便可以得到后验概率:
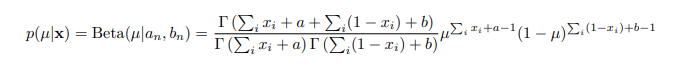
利用Beta分布模型,大大降低了我们维护和更新模型的计算复杂度,也使模型的更新和维护在消费级计算机上的运行成为了可能,下面就利用代码对模型进行一些test。
mu为我们真实概率分布,N为模型更新次数,a,b为我们设定的先验概率,红线为每次维护模型留下的轨迹,蓝线为维护结束后得到的最终模型。
import numpy as np
from scipy.stats import beta
import matplotlib.pyplot as plt
def posterior(a,b,X):
a_n = a + X.sum()
b_n = b + (X.shape[0]-X.sum())
return beta.pdf(mu_test,a_n,b_n)
# parameters to generate data
mu = 0.9
N = 200
# generate some data
X = np.random.binomial(1,mu,N)
mu_test = np.linspace(0,1,100)
# now lets define our prior
a = 10
b = 10
# p(mu) = Beta(alpha,beta)
prior_mu = beta.pdf(mu_test,a,b)
# create figure
fig = plt.figure(figsize=(10,5))
ax = fig.add_subplot(111)
# plot prior
ax.plot(mu_test,prior_mu,'g')
ax.fill_between(mu_test,prior_mu,color='green',alpha=0.3)
ax.set_xlabel('$\mu$')
ax.set_ylabel('$p(\mu|\mathbf{x})$')
# lets pick a random (uniform) point from the data
# and update our assumption with this
index = np.random.permutation(X.shape[0])
for i in range(0,X.shape[0]):
y = posterior(a,b,X[:index[i]])
plt.plot(mu_test,y,'r',alpha=0.3)
y = posterior(a,b,X)
plt.plot(mu_test,y,'b',linewidth=4.0)
plt.show()
mu=0.9,N=100时,先验分布为标准正态分布:
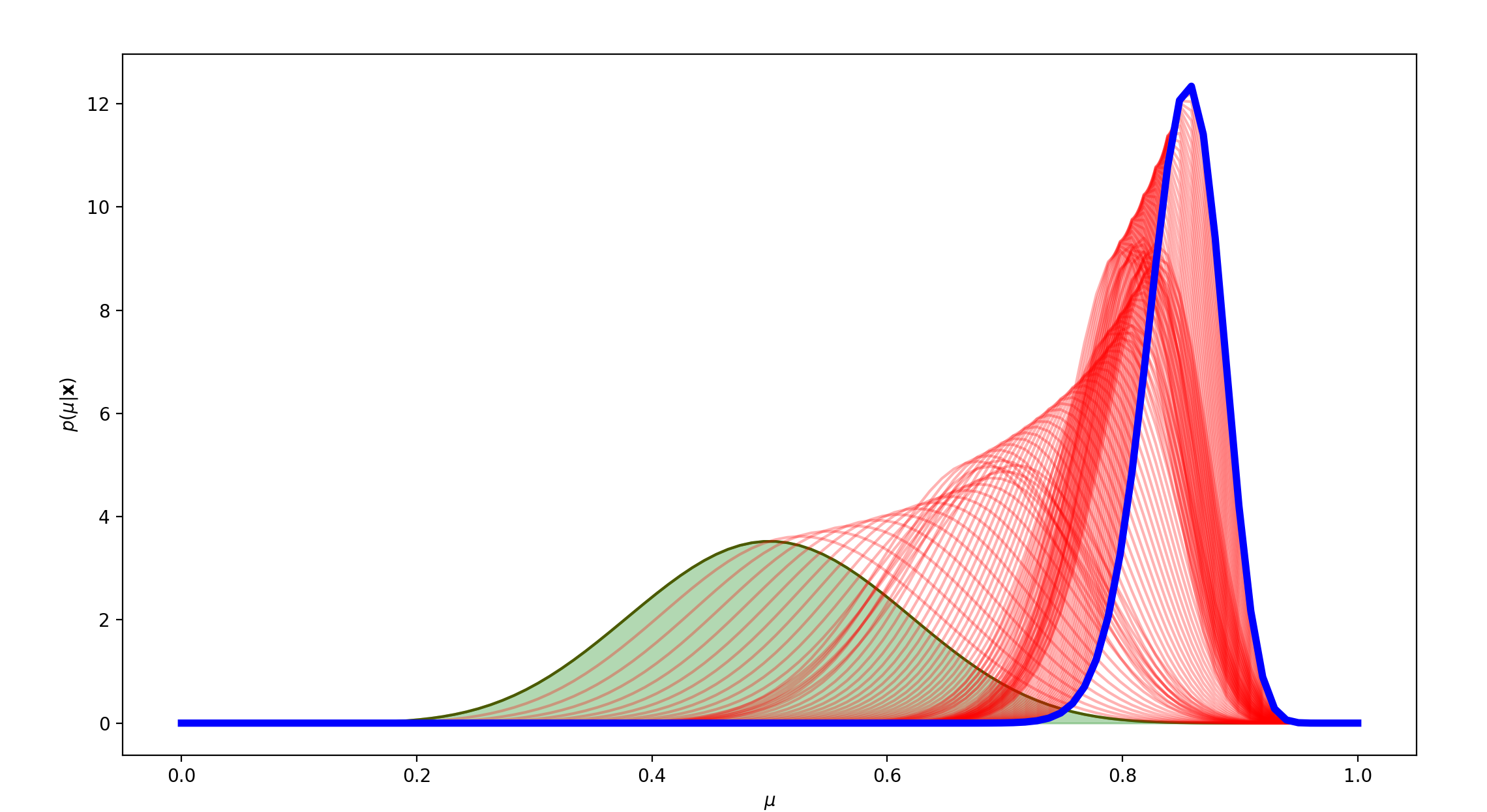
可以看到,在标准正态分布的先验分布下,即使先验分布与真实分布相差甚远时,经过100轮的维护,最终的模型也很贴合真实分布。
mu=0.9,N=100时,先验分布非标准正态分布:
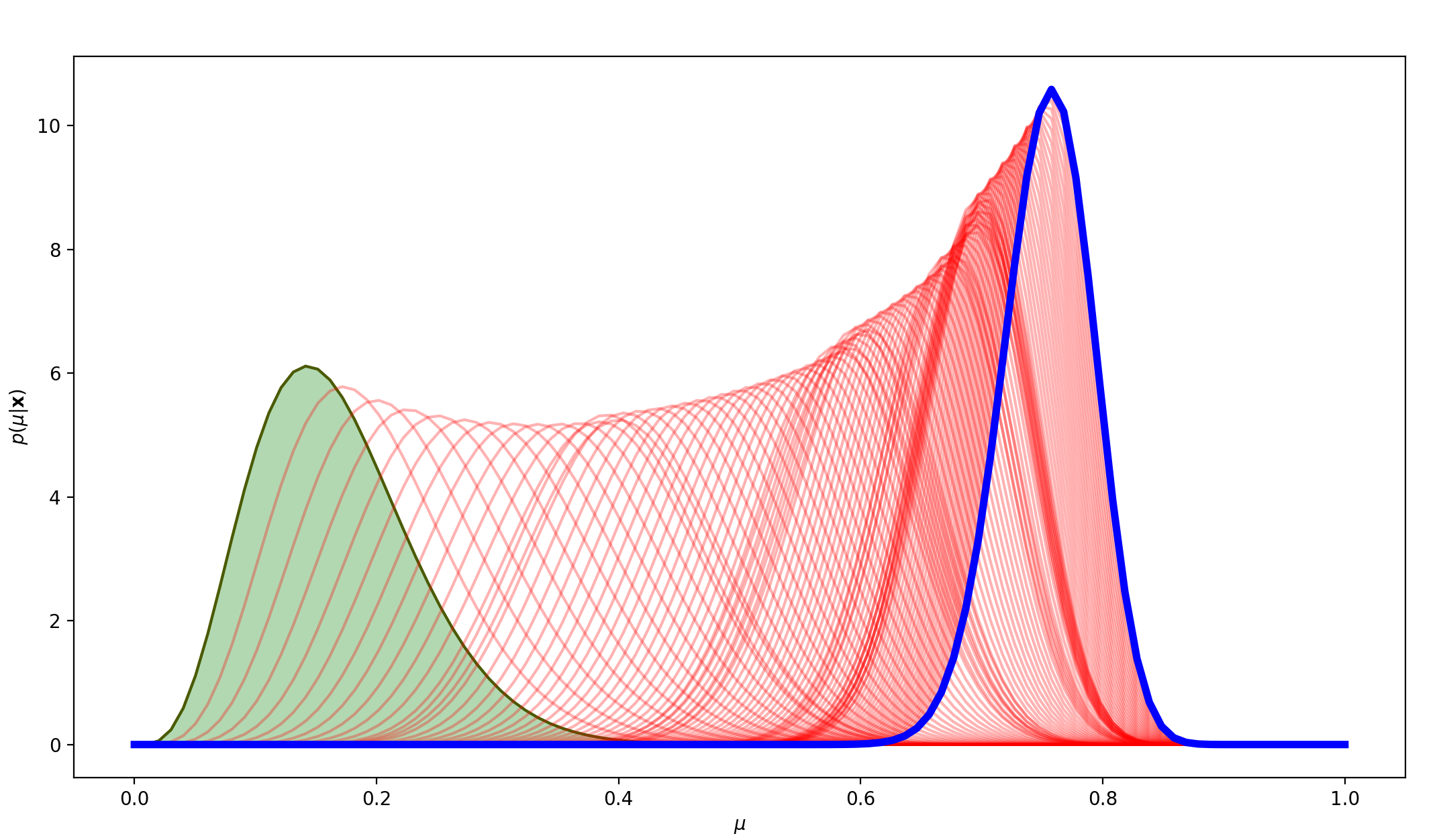
可以看到,在非标准正态分布的先验分布下,由于真实分布与先验分布相差太远,100轮的维护已经不足以获得一个我们满意的模型,需要更多的数据来填补先验分布的误差。
mu=0.9,N=300时,先验分布非标准正态分布:
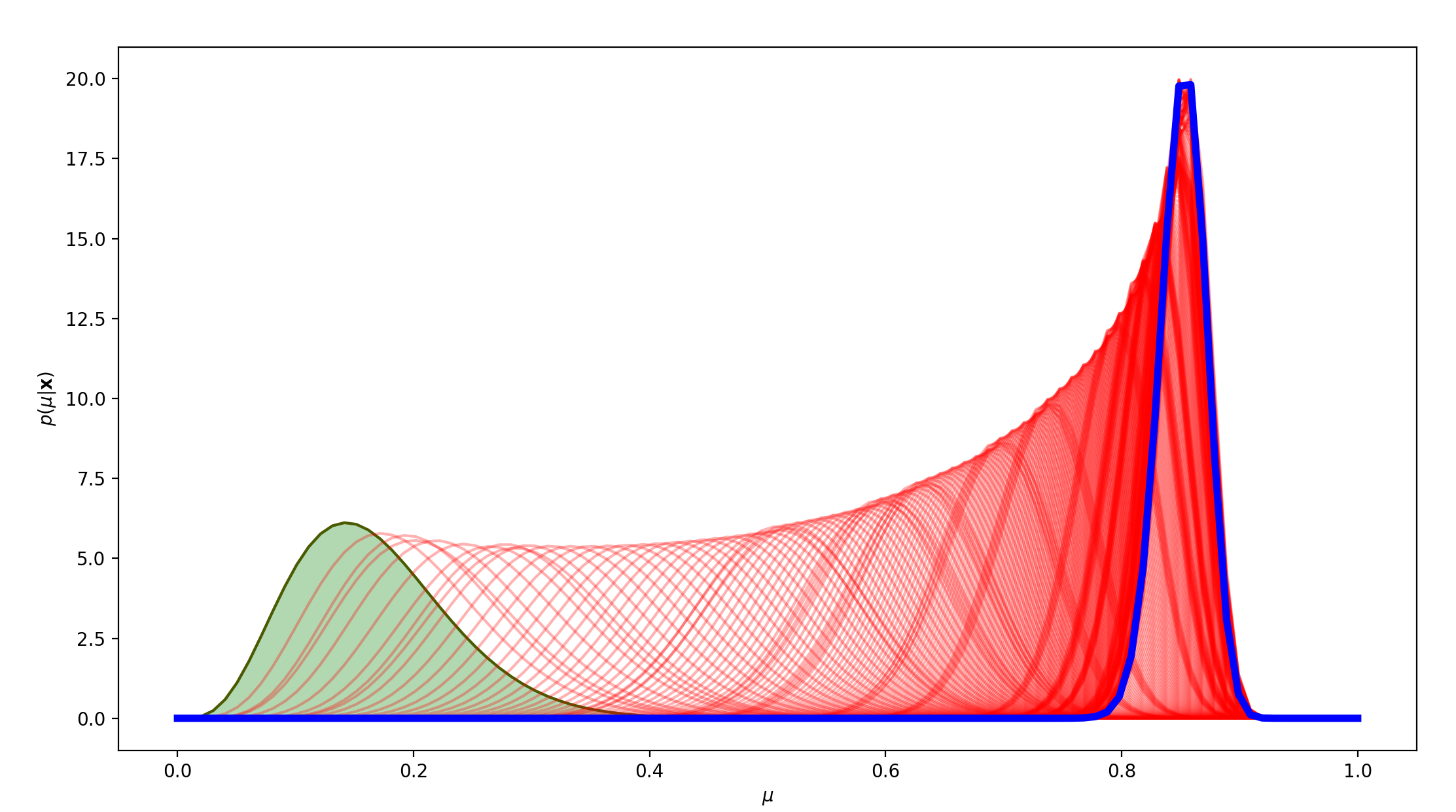
可以看到,在非标准正态分布的先验分布下,即使真实分布与先验分布相差太远,300轮的维护后我们获得的模型大大提升了精准度,逐渐向真实分布靠拢。
mu=0.5,N=50时,先验分布为标准正态分布:
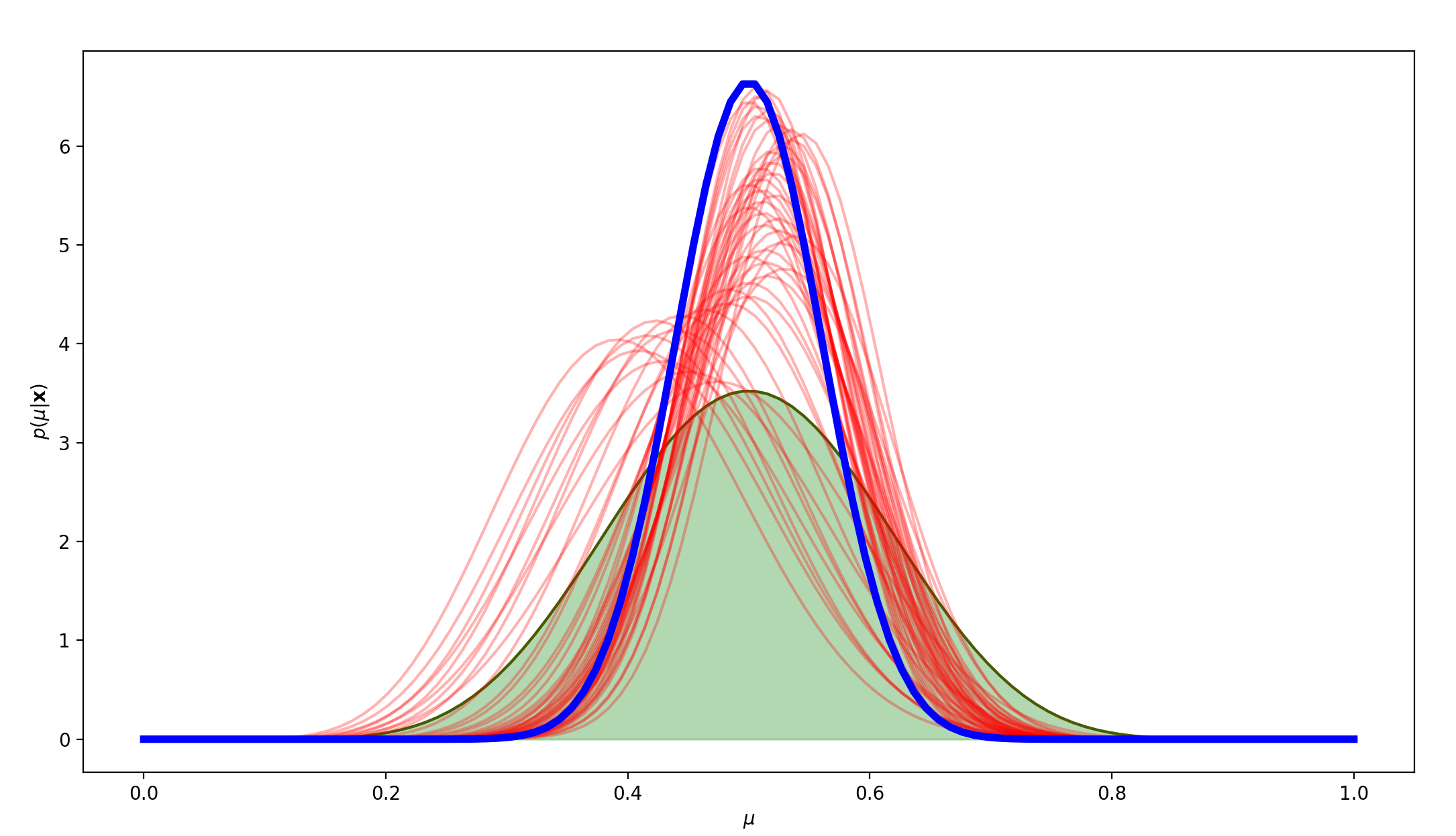
可以看到,在标准正态分布的先验分布下,真实分布与先验分布相同时,在50轮的训练中,虽然在过程中出现了一些偏移,但五十轮之后的结果还是十分准确的。
嘿嘿,就写这么多,走乐🥱。
©著作权归作者所有


