本功能利用Python语言,基于numpy库实现
蒙特卡洛树搜索
要利用蒙特卡洛树对对五子棋棋局进行搜索,首先要了解蒙特卡洛树搜索的过程。
一般来说,蒙特卡洛树的搜索过程分为四步,分别是选择(Selection),扩展(Expansion),仿真(Simulation)和反向传播(Backpropagation),要能让这些操作顺利地运转起来,我们首先需要一个树形数据结构,姑且叫它游戏树。
要实现树形结构,首先要定义节点的数据结构,新建一个节点类型Class Node,代表一个棋盘格局,其属性分别有:
board棋盘格局,
pre_pos最后一次落子的位置,
parent父节点,
children所有的子节点,
not_vistit_pos未访问的结点,
num_visit该节点被访问的次数,
num_of_wins该节点仿真过程中黑子和白子的胜利次数,
属性定义以及初始化如下:
def __init__(self, parent=None, pre_pos=None, board=None):
self.pre_pos = pre_pos
self.parent = parent
self.children = list()
self.not_visit_pos = None
self.board = board
self.num_of_visit = 0
self.num_of_wins = defaultdict(int) # 记录该结点模拟的白子、黑子的胜利次数(defaultdict: 当字典里的key不存在但被查找时,返回0)
仅有数据结构是远远不够的,还需要定义一套动作来实现这些过程:
fully_expanded(self):判断结点是否完全扩展。
non_terminal(self):判断结点是否为终端叶子结点,即该节点对应的格局是否已分出胜负。
pick_univisted(self):选择一个未访问的结点并将其添加进当前结点的孩子中。
pick_random(self):随机选择该节点的一个孩子进行扩展。
num_of_win(self):判断该节点的胜负情况,利用一个实数即可代表黑白二子的胜负差值。
best_uct(self, c_param=1.98):UCT比较过程,选择当前策略下最优的孩子结点,可调节参数,依据的公式为:
\frac{w_i}{n_i} + c \sqrt{\frac{ln t}{n_i}}
w_{i}代表第i次移动后取胜的次数;
n_i代表第i次移动后仿真的次数;
c为探索参数—理论上等于\sqrt {2};在实际中通常可凭经验选择;
t代表仿真总次数,等于所有n_i的和。
函数代码附在博客结尾处。
接下来就可以基于这些的动作,着手进行蒙特卡洛树搜索的编写了。
选择(Selection)
选择操作,即从根节点R开始,连续向下选择子节点至叶子节点L。利用best_uct方法,让游戏树向最优的方向扩展,这是蒙特卡洛树搜索的精要所在。
这一步的操作如图所示(箭头代表这一步的操作):
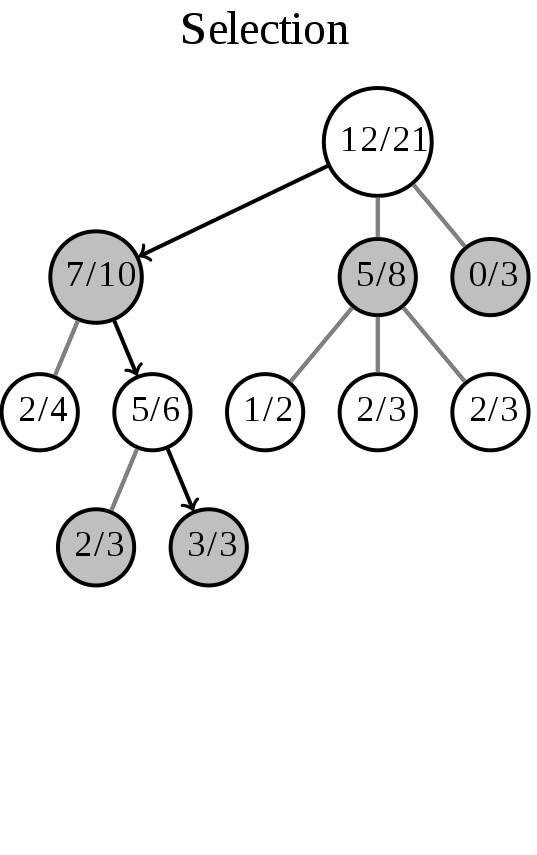
扩展(Expansion)
扩展操作,即除非任意一方的输赢使得游戏在L结束,否则创建一个或多个子节点并选取其中一个节点C。
这一步的操作如图所示(箭头代表这一步的操作):
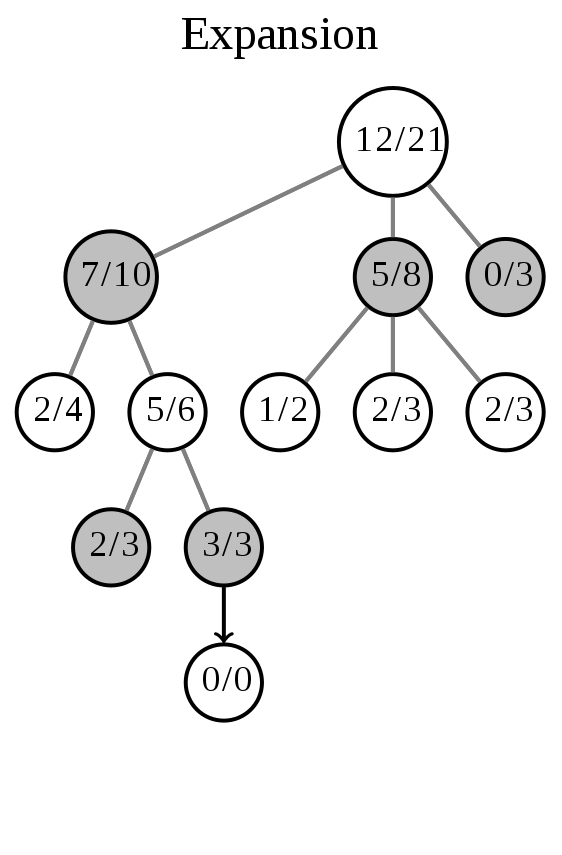
仿真(Simulation)
仿真操作,即在从节点C开始,用随机策略进行游戏,又称为playout或者rollout,直至格局达到终盘,游戏结束,产生胜负。
这一步的操作如图所示(箭头代表这一步的操作):
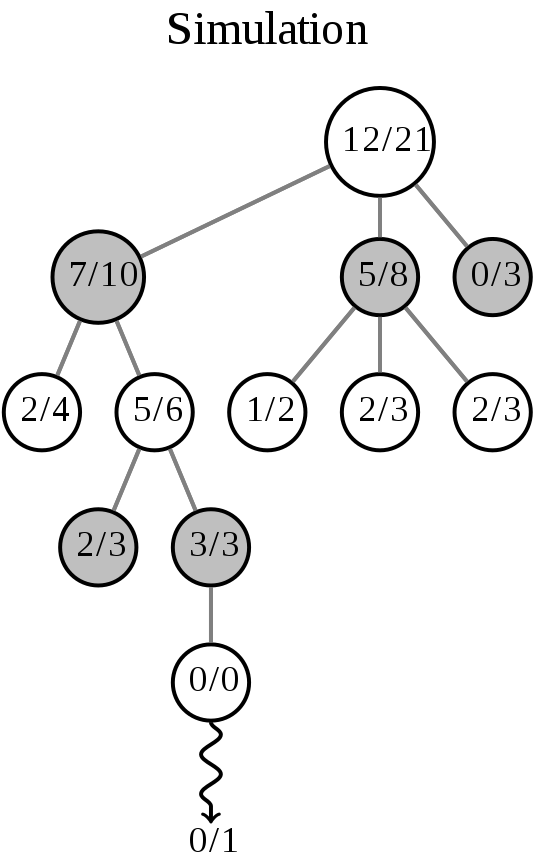
反向传播(Backpropagation)
反向传播操作,即使用上一步仿真随机游戏的结果,更新从C到R的路径上的节点信息,更新每个结点的胜负值以及总盘数。
这一步的操作如图所示(箭头代表这一步的操作):
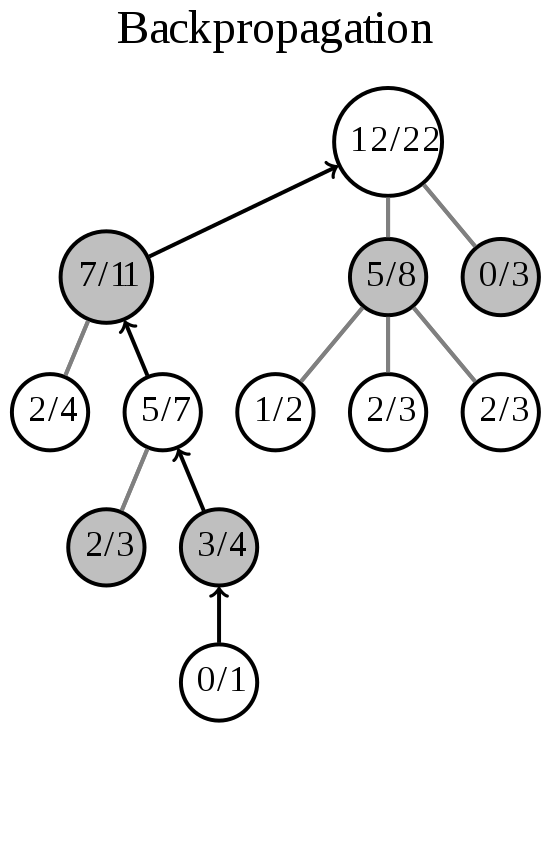
插图中节点内的内容代表胜利次数/游戏次数,我们将利用这个参数来寻找下一步的最优的行棋位置。
根据上述四个步骤,编写函数实现该功能:
traverse(node):遍历结点,遇到已完全展开的结点,利用best_uct选择最佳的孩子节点继续向下遍历。此函数实现选择+拓展过程。
rollout(node):仿真过程,不断利用pick_random()随机选择结点,直至决出胜负,返回胜负值。
backpropagate(node, result):反向传播过程,利用rollout()的结果向上更新节点内容。
best_child(node):利用每个节点的参数(胜利次数/游戏次数)来判断哪一个孩子收益最大,并返回这个孩子。
monte_carlo_tree_search(board, pre_pos):利用上方功能,实现蒙特卡洛搜索,选出最优落子位置。
函数代码附在博客结尾处。
至此,我们已经实现了最基础的蒙特卡洛树搜索功能,接下来就是用户交互界面的编写,这一部分已经与算法无关,仅需不断获取用户的落子位置,并针对每一个棋盘格局,假设用户会选择最有利的位置,对模型进行一定次数的训练,针对训练结果让电脑选择最佳的落子位置。
经初步测试,在6*6棋盘上,每轮经15000次搜索后得到的结果还不错,起码一时半会不会输😂。但在8*8的棋盘上,15000的搜索量就显得有些捉襟见肘,结果不怎么理想。但受限于电脑算力,我也不知道怎么用GPU对这个程序进行运算,再加大搜索量,每次行棋都要等待好长时间,目前就先这样吧,关于用户交互的部分放到下一篇博客吧,有时间就写一个GUI🥱。
*图片来自©维基百科
参考代码:
结点部分:
def fully_expanded(self):
if self.not_visit_pos is None:
self.not_visit_pos = self.board.get_legal_pos()
return True if (len(self.not_visit_pos) == 0 and len(self.children) != 0) else False
def pick_univisted(self):
random_index = randint(0, len(self.not_visit_pos) - 1)
move_pos = self.not_visit_pos.pop(random_index)
new_board = self.board.move(move_pos)
new_node = TreeNode(parent=self, pre_pos=move_pos, board=new_board)
self.children.append(new_node)
return new_node
def pick_random(self):
possible_moves = self.board.get_legal_pos()
random_index = randint(0, len(possible_moves) - 1)
move_pos = possible_moves[random_index]
new_board = self.board.move(move_pos)
new_node = TreeNode(parent=self, pre_pos=move_pos, board=new_board)
return new_node
def non_terminal(self):
game_result = self.board.game_over(self.pre_pos)
return game_result
def num_of_win(self):
wins = self.num_of_wins[-self.board.cur_player]
loses = self.num_of_wins[self.board.cur_player]
return wins - loses
def best_uct(self, c_param=1.98):
uct_of_children = np.array(list([
(child.num_of_win() / child.num_of_visit) + c_param * np.sqrt(np.log(self.num_of_visit) / child.num_of_visit)
for child in self.children
]))
best_index = np.argmax(uct_of_children)
return self.children[best_index]
蒙特卡洛树搜索部分:
def monte_carlo_tree_search(board, pre_pos):
root = TreeNode(board=board, pre_pos=pre_pos)
for i in range(0,mcts_times):
leaf = traverse(root)
simulation_result = rollout(leaf)
backpropagate(leaf, simulation_result)
return best_child(root).pre_pos
def traverse(node):
while node.fully_expanded():
node = node.best_uct()
if node.non_terminal() is not None:
return node
else:
return node.pick_univisted()
def rollout(node):
while True:
game_result = node.non_terminal()
if game_result is None:
node = node.pick_random()
else:
break
if game_result == 'win' and -node.board.cur_player == 1:
return 1
elif game_result == 'win':
return -1
else:
return 0
def backpropagate(node, result):
node.num_of_visit += 1
node.num_of_wins[result] += 1
if node.parent:
backpropagate(node.parent, result)
def best_child(node):
visit_num_of_children = np.array(list([child.num_of_visit for child in node.children]))
best_index = np.argmax(visit_num_of_children)
node = node.children[best_index]
return node
©著作权归作者所有


